Sombreado Realista

Las características de los materiales que contribuyen en el proceso de iluminación son descritas mediante la BRDF.

Existen varios modelos de BRDFs que aportan en mayor y menor medida realismo al material.

Wannabe Amazing es la herramienta interactiva que ha sido desarrollada para el diseño y manipulación de BRDFs. Al mismo tiempo permite asignar de forma selectiva una BRDF a la geometría.

Subir

				Escenas GRF
		• Modelos geométricos existentes – Autocad DXF – Kinetic 3D Studio – WRML – .... • Unificación de características: – Formato interno GRF
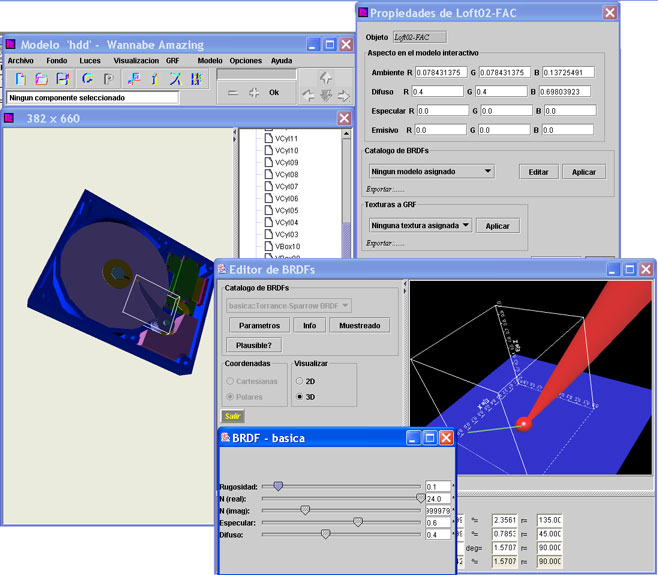
						• Crear una BRDF – Catálogo de BRDFs implementadas • Editar la instancia de BRDF – propiedades – representaciones • 2D : polar • 2D : cartesianas • 3D • Asignar a mallas – Jerarquía de mallas

	Las escenas generadas con WA proceden de modelos geométricos existentes en otros formatos, que serán sintetizados en un formato común de trabajo.
	Una vez creada una BRDF puede editarse para modificar sus propiedades y visualizar los resultados desde varias representaciones.
	La asignación de una BRDF a una malla, propagará esta propiedad a todas las mallas que dependan de la actual.

Subir

			Cambio de dominio: plano [-1,1)2

	Si la BRDF describe el comportamiento de la luz con el material del que esta compuesto el objeto con el que ésta interacciona, deberá considerarse al modelar el transporte de luz. Así la BRDF nos indica cuál es la dirección de salida más probable dada una dirección incidente en un punto de la superficie.

Subir

		Muestrear direcciones de salida utilizando la BRDF como PDF
		• Seleccionar la dirección de salida con mayor energía, en base a una BRDF genérica. • Muestreo eficiente de la BRDF: – Direcciones: de la semiesfera al plano – Subdivisión adaptativa de la función: quadtree – Muestreado por importancias

	El problema con el que nos encontramos es el de la selección de la dirección mas probable de salida que se considera que se producirá al evaluar la BRDF para un vector incidente conocido.
	El muestreo de la BRDF se mejora con dos técnicas para la reducciσn de la varianza. Se construye un quadtree para dividir el dominio en regiones, que contienen direcciones de salida mapeadas en un circulo inscrito en el plano base.
	Usando un descenso estocástico del quadtree podemos seleccionar la región más probable, para posteriormente utilizar solo en dicha región un muestreado por importancias y de esa forma devolver la dirección mas probable.

Subir

Subdivisión Adaptativa

• El dominio se divide en regiones disjuntas que corresponden a los nodos hoja de un quadtree

• El descenso por el quadtree se realiza de forma estocástica, utilizando la probabilidad acumulada hasta llegar la región más probable.

Subir

		Muestreado por Importancias
		• Usamos la técnica de rejection sampling en la región seleccionada – Seleccionamos aleatoriamente un punto (x,y) en la base de la región, correspondiente a una dirección. – Seleccionamos aleatoriamente una altura (z). – Si al evaluar la funciσn z queda por debajo se acepta la muestra.
			– En caso contrario se rechaza y se repite la operación.

Subir

		Comprobación de resultados
		• Numéricamente: Para un número alto de muestras, el número de impactos en una zona, equivale a la integral de la función en dicha región.
			• Gráficamente: Implementando un path tracer y comparándolo con otras PDFs

Subir