1.1. Descripción del problema.

Objetivo: se pretende programar una versión distribuida de la famosa criba de Erastótenes para la obtención de los N primeros números primos.

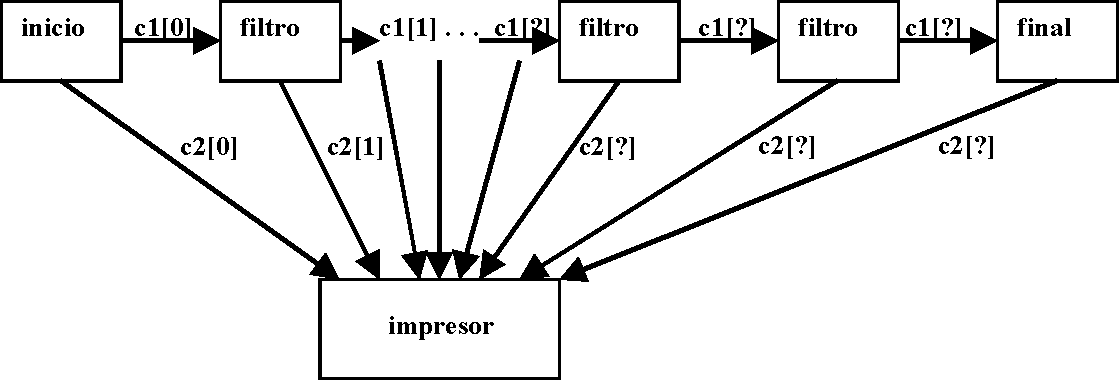
Se utilizará una red de procesos concurrentes conectados como un encauzamiento ('pipeline') de procesos, como el que se muestra en la siguiente figura:

Dado que pretendemos generar sólo los N primeros números primos, se ha de conocer una constante ( nLimite) que es mayor o igual que el N-ésimo número primo.

El proceso inicio de la figura genera el primer número primo (el 2) y lo envía por su canal print para que el proceso impresor lo imprima; después genera el siguiente número primo ( el 3), lo envía el primer proceso filtro del encauzamiento y continúa enviándole valores: 5, 7, 9, ...

Cada proceso filtro comienza su ejecución recibiendo un valor primo del proceso anterior y enviándolo por su canal print respectivo; después recibirá continuamente números, no necesariamente primos, desde el proceso anterior; si el número recibido es divisible por el valor primo que recibió al principio lo descarta, si no, lo envía al proceso filtro siguiente. El proceso final recibe el último número primo, lo envía por su canal print y después descarta los demás números que reciba.

El proceso impresor recibe los valores primos de los N procesos del encuzamiento en un orden no-determinístico y los muestra en la pantalla ordenados.
 

1.2. Descripción del problema.

Un autobús sigue la misma ruta cada día y tiene N paradas, numeradas 0, 1, 2, 3, ..., N-1. Supongamos un conjunto de M pasajeros, cada uno de ellos con un número que indica la parada donde se sube al autobús y otro que indica la parada en la que se baja (supongamos, además, que cada uno de los pasajeros comunica el número de parada de subida al conductor del autobús por teléfono, ya que el autobús no se detendrá si no recibió previamente el número de parada en una comunicación de un pasajero).

La actuación de los pasajeros es la siguiente: indica el número de parada donde quiere subirse al autobús, espera hasta que el autobús llegue a esta parada, se sube al autobús y, al mismo tiempo, le indica al conductor el número de parada donde se quiere bajar. El pasajero no puede bajarse del autobús hasta que llega a la parada de bajada que le indicó al conductor.

Cuando el autobús llega a una parada no continúa su viaje a la siguiente parada  hasta que todos los pasajeros que indicaron dicha parada, para subirse o bajarse, se han subido o se han bajado, respectivamente. Téngase en cuenta que la capacidad del autobús es limitada.

Se pide-> programar clases en Java, para el proceso autobús y para los clientes, teniendo en cuenta las siguientes condiciones de implementación, para obtener una solución admisible del problema:
 

• La clase-proceso 'autobús' puede recibir mensajes de cualquier proceso-pasajero, por lo tanto, ha de declarar como un parámetro de su método constructor un array abierto de canales. La longitud actual de dicho array será establecida posteriormente en la clase principal del programa (en el método:  public static void main (...)).
• En la clase autobús hay que incluir las siguientes variables: el número de la última parada del autobús, el número de parada de subida y de bajada de cada pasajero, el número de pasajeros que se subirán y se bajarán en cada parada (ya que el el autobús ha de saber cuantos pasajeros quedan por subir o bajar en la parada actual, para decidir continuar a la parada siguiente o seguir esperando).
• Los pasajeros no pueden bajarse o subirse del autobús hasta que este llegue a la parada que previamente comunicaron.
•  Los pasajeros generarán de forma aleatoria: Math.abs(randGen.nextInt() % numeroParadas); los números de parada para subirse o bajarse del autobús, que comunicarán al proceso-autobús.
• Los mensajes, indicando el número de parada de subida, que envían los procesos pasajeros al proceso autobús tienen prioridad sobre los otros (2) mensajes que los procesos clientes envían.

 

1.3.1. Ordenación por encauzamiento.

El algoritmo de ordenación mediante un encauzamiento ('pipeline sort') consiste en implementar un encauzamiento de procesos paralelos que es alimentado con una secuencia desordenada de caracteres. El resultado a la salida del último proceso es la secuencia de caracteres ordenada.

Cada proceso o elemento del encauzamiento tiene capacidad para almacenar un carácter (que será el mayor número recibido hasta el momento): en cada iteración, recibe un carácter por su canal de entrada, lo compara con el que tenía almacenado, y el menor de ambos es enviado por su canal de salida al próximo elemento del encauzamiento, mientras que el mayor es almacenado.

Estudiar el siguiente escenario para entender el funcionamiento del algoritmo:

1. Supongamos que en un instante dado de la ejecución, los tres primeros elementos del encauzamiento tienen un carácter almacenado ('f', 'c' y 'a', respectivamente), mientras que el cuarto aún no ha recibido ninguno.

1. Ahora supongamos que se recibe el carácter ‘b’ por el canal de entrada al encauzamiento.

1. El primer proceso compara el valor recibido con su valor almacenado, envía el menor de ellos (‘b’) por su canal de salida, y almacena el mayor (‘f’).

1. De la misma forma el segundo proceso, tras recibir el carácter enviado por el primer proceso (‘b’), lo envía por su canal de salida y mantiene almacenado el carácter ‘c’.

1. El tercer proceso, sin embargo, envía el carácter que tenía almacenado (‘a’) por su canal de salida y almacena el que acaba de recibir (‘b’).

1. El cuarto proceso, al no tener todavía ningún carácter almacenado, se guarda el recibido por su canal de entrada (‘a’)

 
2. Ahora supongamos que se recibe el carácter 'g' por el canal de entrada del encauzamiento, el primer proceso enviará 'f', que tenía almacenado, y almacenará 'g'.

 
3. Entonces el segundo proceso recibe 'f', lo almacena, y envía 'c'.

 
4. El tercer proceso recibe 'c', lo almacena, y envía 'b'

 
5. El cuarto y último proceso recibe 'b', lo almacena y envía el carácter 'a' que tenía almacenado por su canal de salida.

 
6. y así sucesivamente, ...

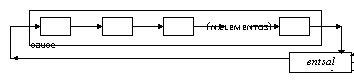
Para formar el encauzamiento, se lanzarán en paralelo los elementos del encauzamiento conectados como se indica en la figura. El proceso entSal lee la secuencia de caracteres por teclado, los envía uno a uno al encauzamiento y los recibe ordenados para después imprimirlos por pantalla. El esquema de conexión general es el de la figura siguiente:

Clasificación por burbuja secuencial:

Este algoritmo consta de varias fases. En cada fase, la matriz se recorre de izquierda a derecha y cualesquiera elementos vecinos fuera de orden son intercambiados. El resultado es que el elemento mayor es desplazado a la última posición. Después de cada fase, la parte clasificada (en este caso está al final de la matriz) aumenta. Considérese el siguiente ejemplo:

 
1   6   3   2      -- matriz inicial
-----
1   6   3   2
    ----- intercambio
1   3   6   2
        ----- intercambio
1   3   2   6      -- el elemento mayor queda al final
            ^
1   3   2   6      -- segunda fase
-----       ^

1   3   2   6
    -----   ^  intercambio
1   2   3   6      -- 3 y 6 situados correctamente
        ^   ^
1   2   3   6      -- tercera fase
-----   ^   ^
1   2   3   6      -- matriz ordenada
^   ^   ^   ^
 

Como hemos visto, la clasificación por burbuja secuencial consta de una serie de fases en las cuales el elemento mayor burbujea hasta el fin. El algoritmo secuencial ejecuta las fases una tras otra, pero las fases prodrían intercalarse también, como muestra el ejemplo siguiente:

 
5   4   3   2   1      -- primer paso, fase 1
--1--
4   5   3   2   1      -- segundo paso, fase 1
    --1--
4   3   5   2   1      -- tercer paso, fase 1
        --1--
4   3   2   5   1      -- cuarto paso, fase 1
--2--       --1--      -- primer paso, fase 2
3   4   2   1   5      -- segundo paso, fase 2
    --2--       ^
3   2   4   1   5      -- tercer paso, fase 2
--3--   --2--   ^      -- primer paso, fase 3
2   3   1   4   5      -- segundo paso, fase 3
    --3--   ^   ^
2   1   3   4   5      -- primer paso, fase 4
--4--   ^   ^   ^
1   2   3   4   5      -- matriz clasificada
^   ^   ^   ^   ^

Se puede realizar esta ejecución por medio de un encauzamiento:

Hemos definido el intercambiador de tal forma que el encauzamiento clasifica una secuencia en orden descendente. Esto hace más obvia la semejanza con la clasificación por burbuja secuencial. Podemos redefinir fácilmente el intercambiador para clasificar la secuencia en orden ascendente. En lo que sigue, resolveremos un ejemplo que demuestra el funcionamiento del cauce. Hemos elegido deliberadamente mostrar el funcionamiento del cauce de una manera muy secuencial con objeto de acentuar su similaridad con el algoritmo de clasificación por burbuja. Normalmente, un encauzamiento funciona de una forma más paralela.

Debido a que el intercambiador es determinista, el resultado verdadero no depende de la secuencia de cálculo.

Suponga que los valores 5,3,4,6,2 son introducidos en un encauzamiento como este:

El proceso 'id' copia su entrada sobre su salida:
 

El intercambiador final lee sus entradas, las compara, y deposita el número mayor (5) en el canal de salida izquierdo y el número menor en el canal de salida derecho.


El tercer intercambiador intercambia su entrada.


El segundo intercambiador permuta su entrada. Como ahora 6 es el mayor, se pone en el canal de salida izquierdo y 5 se deja en el canal de salida derecho.


El primer intercambiador cambia su entrada.


El encauzamiento ha ejecutado ahora la primera fase de la clasificación por burbuja.
 

El cálculo continua con la segunda fase, como sigue:




La segunda fase esta completa. Ahora, empieza la tercera fase.





La tercera fase esta completa. Ahora empieza la cuarta fase.
 




Finalmente, se copia el último elemento.


 

 
Sugerencia:
• Podemos introducir valores en el encauzamiento si cada intercambiador envía un valor muy grande en su canal de salida derecho, antes de que se  inicie realmente el intercambio con los valores que se quieren ordenar.

 
• Los valores pueden desplazarse fuera del encauzamiento si se depositan sobre el canal de entrada del encauzamiento algunos valores muy pequeños, después de que se hayan recibido los valores verdaderos. Utilice un valor de entero más pequeño que los datos a ordenar para descargar el encauzamiento, después de que se ejecute la última fase del algoritmo.

 

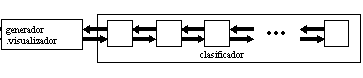
El proceso generador.visualizador recibe la secuencia ordenada y la muestra sobre la pantalla. Dicha secuencia está precedida por un grupo de enteros muy grandes, que deben ser descartados antes de la visualización de los resultados.