MODELIZACION Y VERIFICACION DE UN ALGORITMO
CONCURRENTE
UTILIZANDO LA NOTACIÓN:
SENIL
(Simple Extensible Net Input Language)
.
1. Descripción
del problema
1.2. Descripción del
lenguaje SENIL
1.3. Utilización del
programa check
1.4 Ejercicio 1.1
1.5 Ejercicio 1.2
1.6 Proposiones
atómicas
Grafo completo de
la red
1.1.
Descripción del problema.
Se pretende modelizar el algoritmo para resolver
el problema de la exclusión mutua de Dekker mediante una red de
Petri segura (marcado lugares 1-limitado). También se procurarán
verificar las propiedades del modelo obtenido, de una manera similar a
lo realizado en prácticas anteriores sobre 'model checking'.
1.2. Descripción
del lenguaje SENIL.
Es un lenguaje adecuado para describir redes de Petri seguras (todos
sus lugares son 1-limitados) de un tamaño no muy grande, un máximo
de aprox. 100 nodos. Se pretende codificar las redes de Petri directamente
en este lenguaje, ésto es no vamos a utilizar ningún editor
gráfico. No se necesita, para utilizarlo, más que conocer
conceptos básicos acerca de redes de bajo-nivel (redes lugar-transición).
Hablando de forma general, los datos necesarios para poder definir redes
de Petri seguras será sólo información (de tipo textual)
referida a: lugares, transiciones, arcos y marcado inicial de la red.
Por lo tanto, más abajo se puede observar qué elementos
sintácticos tiene el lenguaje para definir una red de Petri segura:
SENIL
@trans
P1, ... -> T1{@label, ... } -> P3, ...
# T1 -> P1, ...
P1, ... -> T1 #
@place
T1, ... -> P1 -> T2, ...
# P1 -> T1, ...
T1, ... -> P1 #
@marking
P1, P2, P3, ...
@partition
P1, P2, P4, ...
P3, P5, P6, ...
.
.
.
-
La descripción de una red debe comenzar con la palabra reservada
SENIL.
-
Se pueden describir las redes de Petri desde el punto de vista de las transiciones,
listando los preset o conjuntos de lugares de entrada y los postsets
o conjuntos de lugares de salida de las transiciones de la red. El símbolo
especial @trans indica el comienzo de un bloque del 'programa-senil'
en el que cada línea contiene la especificación de una transición
(cuya etiqueta se encuentra rodeada por flechas (->)). Cada una de las
líneas comienza con la lista de lugares contenidos en el preset
de la transición y termina con la lista de lugares contenidos en
el postset de la referida transición. Los presets
o postsets vacíos (transiciones que no tienen lugares de
entrada o de salida) se denotan mediante los símbolos #
or '.'. Por ejemplo, la línea P1, P9 -> T1 ->
P2, P10 significa que existen arcos desde los lugares P1
y P9 a la transición
T1 y de la transición
T1
a los lugares P2 y P10.
-
De forma alternativa, se puede describir una red desde el punto de vista
de los lugares, listando los presets o conjunto de transiciones
de entrada y los postsets o conjuntos de transiciones de salida
de los lugares de la red detrás de la sección que comienza
con el símbolo especial @place. En este caso, los
nombres de los lugares se encuentran entre flechas (->) y las transiciones
de los conjuntos preset y postset se indican antes y después
de los lugares, respectivamente. Téngase en cuenta que el conjunto
preset
o postset, o ambos, pueden estar vacíos, en cuyo caso deben
ser re-emplazados por el símbolo # o '.'.
Los lugares marcados inicialmente se listan detrás de la palabra
reservada @marking. Se suelen listar al final del 'programa-senil',
todos los lugares marcados inicialmente. En el ejemplo del algoritmo de
Dekker, representado en la figura siguiente, sería: (P1,
P9,
P11,
P13,
P15).
-
Algunas herramientas pueden hacer uso de informaciones adicionales que
se refieren a particiones de lugares de la red. Cada línea del 'programa-senil'
que aparece después de la palabra reservada @partition
define una lista de lugares que forman una partición.
-
A veces es muy útil suministrar transiciones o lugares con
información complementaria, tal como etiquetas, etc. Cada transición
o lugar puede ser seguida de una información adicional entre llaves
( @label "xxxxxxx", ...) con difrentes campos separados
por comas. Cada información complementaria debe ser indicada con
una palabra reservada especial. Por ejemplo, la etiqueta de una transición
puede ser indicada mediante T1 {@label a}.
El lenguaje es fácilmente extensible ya que cada información
adicional necesaria para nuevas especificaciones puede ser añadida
definiendo una palabra reservada especial nueva anates de la nueva información.
1.3. Utilización del programa
check
con SENIL
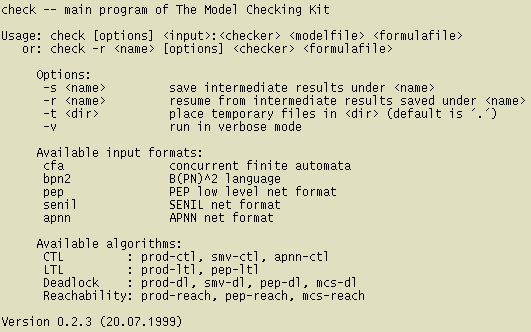
Se pide->
-
Hay que modelizar el algoritmo de Dekker
en SENIL. Para ello necesitaremos el algoritmo descrito como una red
de Petri segura.
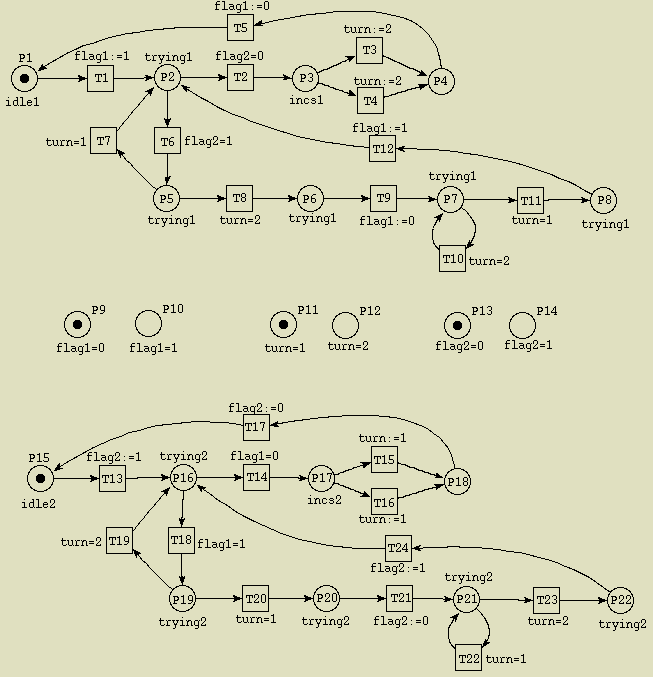
Los lugares del P9 al P14 denotan los distintos
valores que pueden tomar las variables del algoritmo de Dekker. Por ejemplo,
si el proceso 1 dispara la transición T1, entonces el valor
de la variable flag1 debería ser 1. Es más,
sabemos que el valor de flag1 es
0 antes de la ejecución
de T1. Para modelizar este comportamiento dinámico correctamente,
hemos de dibujar arcos de P9 a T1 y de T1 a
P10.
La transición
T2 debería se disparada sólo
si el proceso 1 permanece en el estado P2 (se encuentra marcado)
y si el valor de la variable flag2 es
0 antes de la ejecución
de T2. Por lo que hemos de dibujar un arco de
P13 a T2.
También, hemos de dibujar un arco de T2 a
P13 ya que
el valor de flag2 no puede ser cambiado durante la ejecución
de T2.
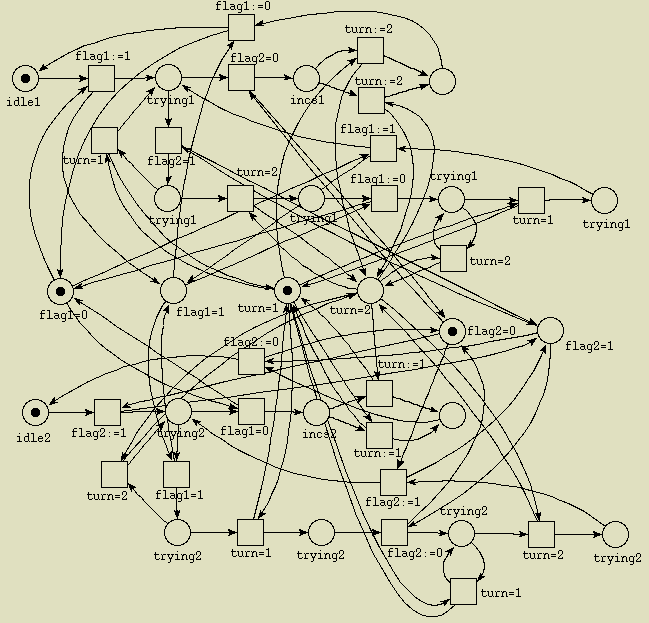
Con el motivo de no hacer demasiado complejo el gráfico, se han
omitido todos los arcos de la red anterior que conectan los lugares P9
a
P14.
Mirar más abajo si se quiere ver la
red completa.
Con la información del grafo de la red, ha de ser relativamente
fácil modelizar el algoritmo de Dekker utilizando SENIL.
-
Utilizar los algoritmos: pep-dl, prod-dl,
smv-dl, mcs-dl , para demostrar que el algoritmo de Dekker está
libre de interbloqueo. Así como los algoritmos: prod-ltl, pep-llt,
prod-ctl, etc., para comprobar las propiedades de vivacidad del algoritmo.
Proposiciones atómicas en formulas
Las proposiones atómicas pueden consistir en ...
-
Nombres de lugares
Un nombre de lugar puede ser uan proposición atómica,
por ejemplo P1, P2, P3.
-
Etiquetas de lugares
Se puede usar la etiqueta de un lugar como una proposición atómica,
por ejemplo
"incs1".
Las etiquetas deben de ir entre comillas.
Grafo completo de la
red de Petri segura que representa el A. de Dekker.